Cutting Gas Costs with Smart Ethereum Address Choices

Gas costs are a critical factor in any blockchain project. Every transaction, comes with an inherent price tag. While there are numerous ways to optimize these costs, one method that often flies under the radar is selecting Ethereum addresses with specific characteristics to reduce gas consumption.

At first glance, it might seem that the address you use in a transaction wouldn’t have any impact on gas fees. However, this isn’t true. Ethereum transactions often require passing addresses as part of the transaction data. When these addresses are encoded into the transaction data, the cost of encoding a zero byte is significantly less than that of encoding a non-zero byte.

Ethereum Word Composition and Storage

In the EVM, data is stored and processed in chunks of 32 byte words. Every piece of data, including addresses, must be encoded into this format before being stored or processed.When interacting with the EVM, storing or manipulating these words can be costly, especially when they contain non-zero bytes. For example:

Transaction Data: When sending a transaction that includes data (e.g., a function call with parameters), the data is encoded into bytes. Each byte in this data is charged based on whether it is zero or non-zero.

• Zero bytes cost 4 gas each.
• Non-zero bytes cost 68 gas each.

Consider the following two addresses:

• Address A: 0xdecafbad00000000000000000000000000000000
• Address B: 0x1234567890abcdef1234567890abcdef12345678

EVM words default to zero, so avoiding non-zero bytes reduces gas costs. The hamming weight, which measures the number of non-zero bits in data can be used to measure how many extra stores can be saved. Address A has a lower Hamming weight because it contains more zero bytes, as a result, using Address A in a transaction incurs lower gas fees compared to Address B.

Browser solutions

Websites like vanity-eth.tk expose the concept easily over the browser but have the disadvantage that trying to run brute-force inside the browser is crazy inefficent, and we’re trusting that they don’t send a response to their server. The latter can be mitigated by disconnecting from the internet temporarily and flushing the browser cache afterwards. Even if we assume the website is safe and doesn’t send our newly generated private key across the network, we can’t be so sure than they’d never be compromised in the future.

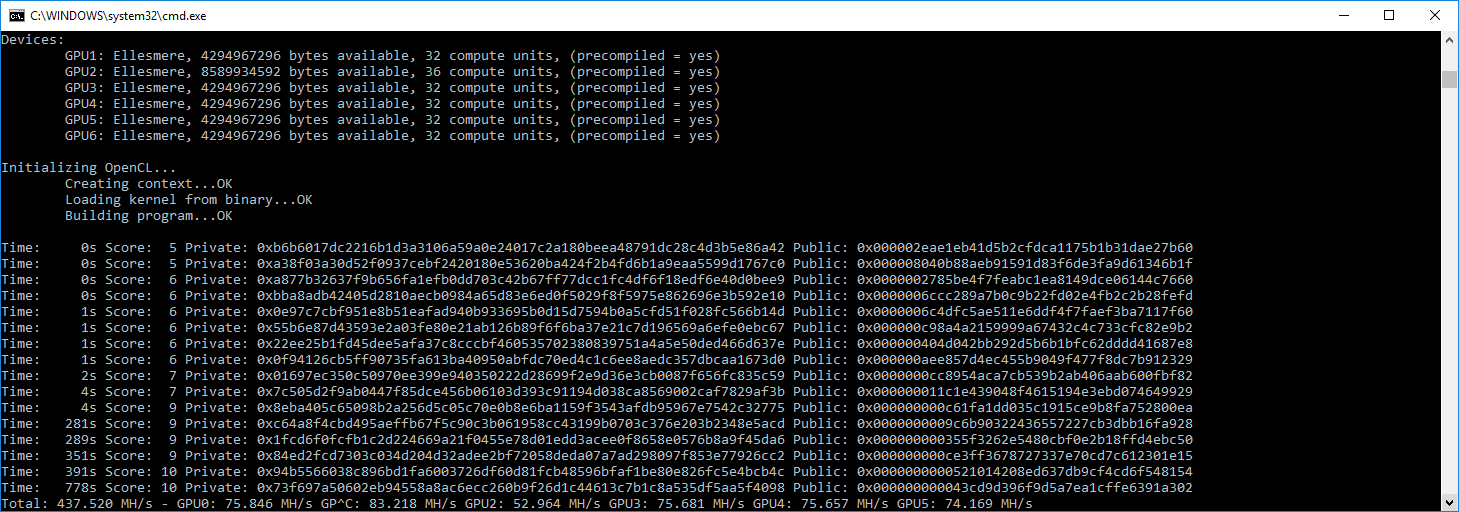
One winter I spent 3 continuous days trying to generate an 8 leading zero on an NVIDIA GTX TITAN using vanity-eth.tk which was a very electricity expensive operation. Nowadays I can generate hundreds in less than 5 minutes on my M1.

Generating leading zero addresses with Profanity2

Profanity2 is one of the fastest open sourced Ethereum vanity address generators which can find specific patterns or sequences, such as leading zeros or custom prefixes and suffixes. It works by leveraging brute-force techniques to find private keys that, when hashed using keccak-256, produce an address that matches the desired pattern.

Profanity2 requires a user provided public key which will change hex bytes and generate a new private key from them, profanity2 then computes a new Ethereum address from this manipulated public key, checking it against some specified criteria. Once a match is found, a private key which is offset from the original private key is produced. We’ll need both our original public/private key, and our generated private key

This demonstration can be easily replicated by reading through 1inch/profanity2’s readme. For those who can’t decypher the readme, my tutorial might be more digestible.

1. Grab any old private key you have laying around or generate a new wallet using metamask and get it’s private key. We’ll use openssl to derive a public key from that. Remove any prefixing ‘0x’ from the private key.
   openssl ec -inform DER -text -noout -in <(cat <(echo -n "302e0201010420") <(echo -n "PRIVATE_KEY_GOES_HERE") <(echo -n "a00706052b8104000a") | xxd -r -p) 2>/dev/null | tail -6 | head -5 | sed 's/[ :]//g' | tr -d '\n' && echo
2. That will return a 130 byte hexadecimal public key, ensuring that the prefixing ‘04’ is removed, we should be left with 128 bytes.
3. Clone the 1inch/profanity2 to your machine.
   git clone https://github.com/1inch/profanity2.git
4. Running the command which will find –leading 0’s. The -z flag is the seeding public key for the bruteforcing.
   ./profanity2.x64 --leading 0 -z DERIVED_PUBLIC_KEY_GOES_HERE

Profanity generating 10 leading zeros in just over 2 hours. Notice how the private key ending is mutated.

5. Once you’re happy with an address that’s been generated you can stop the search and run the command, removing the prefixing ‘0x’ from the newly generated PRIVATE_KEY_2.
   (echo 'ibase=16;obase=10' && (echo '(PRIVATE_KEY_1 + PRIVATE_KEY_2) % FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F' | tr '[:lower:]' '[:upper:]')) | bc

What happened to Profanity1?

In September 2022, the original Profanity’s vanity addresses fell victim to an attack. Exploiting a flaw in the tool’s key generation process, attackers drained $3.3 million worth of tokens from users’ wallets.

Profanity used a pseudorandom number generator seeded with an unsigned integer, limiting the possible seed values to approximately 4.3 billion. Although this number might seem large, it was not enough to prevent brute force attacks. Estimates suggested that a setup of 1,000 GPUs could potentially crack the private keys of every 7-character vanity address generated by Profanity within 50 days. While costly, the potential rewards were significant.

In early 2022, 1inch researchers discovered and reported this vulnerability in Profanity. However, the issue gained widespread attention only after attackers exploited it, stealing $3.3 million in tokens and putting additional addresses at risk.

Read the full article released on 1inch’s blog.

What is a Merkle tee?

A Merkle tree is a data structure which shares some qualities of a binary tree and a distributed hash table.

A Merkle tree is similar to a binary tree, whereby the graph has a branching factor of 2 - each node is expected to have 2 children and end with one root node. A Merkle tree has the following time difficulty properties across all scenario cases.

The qualities that a Merkle tree inherits from a distributed hash table is that the parent node value is the result of some hashing function using the two child nodes. If either value is changed in the children, then the parent’s resulting value will also be different.

This changed hash will propogate and be used in other hashing functions, resulting in the root being different. This is how the Merkle tree ensures the validity of child nodes values across a large data set.

What are Merkle trees used for?

Merkle trees are often used in decentralised storage, where the goal is to store data over a network of machines.

Because of the hashing quality of a Merkle tree, they are able to hash a large dataset into many fixed sized hashes during tree creation and then are able to pass around a single parent root node, collated of all the previous hashes.

Since Merkle trees can verify a single leaf node inclusion in logarithmic time - less overall data and overhead is needed to prove this inclusion - and this is why Merkle trees are popular in crypto token distributors.

Example of constructing a Merkel tree

When creating a Merkel tree, an inital data is hashed to produce a set of leaf nodes. The leaf nodes are shown as h1 … h4 in the diagram below. The inital leaf data could be :

• Segmented parts of a file
• A list of transactions as a part of a blockchain block
• Other large blobs of user defined data whereby logarithmic time lookups can be done

Taking the leaf nodes in pairs like in a binary tree, we create a parent node which is the result of concatenating and hashing the children h1 and h2. This is done until the tree is formed and we are left with one parent root node h1h2h3h4.

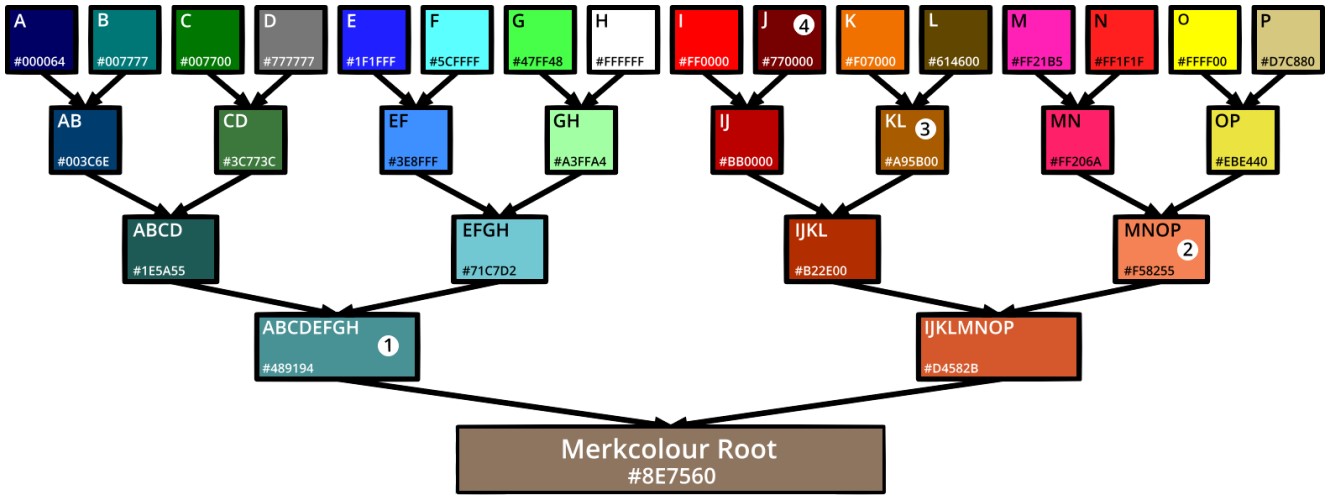
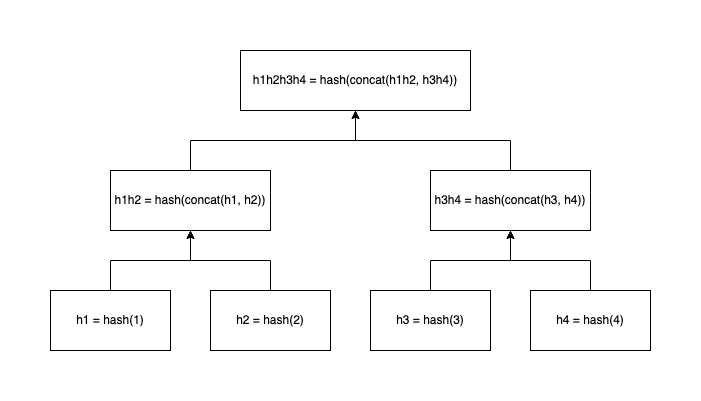A balanced Merkel tree with an even number of leaf nodes.

Advantage 1 - Root checksum

The root hash is a derived calculation from the inital leaf data. If a character of data in a leaf node changes then the hash calculated for the leaf will be different, cascading in hash changes down the branches resulting in a different root hash being present. The root is able to be used as a checksum that all of the leaf data are byte-perfect and free from corruption or changes.

If an odd number of input nodes are present at any branch of the tree - then the properties of a binary tree aren’t fulfilled. The Merkel tree should duplicate the orphaned node and hash it with itself. In the below example, the duplicated nodes that are used to balance the tree are highlighted in orange. h5 has no sibling so is duplicated and hashed with itself to create a parent h5h5. h5h5 also has no sibling, so it is duplicated and hashed with itself to create a parent h5h5h5h5. At this branch a sibling exists for h5h5h5 so no duplication is required.

A unbalanced Merkel tree with an odd number of leaf nodes.

The naieve way of checking is to generate a new tree from all nodes, in our example these are h1 … h8 and checks that when generating a Merkle tree that the old root and the new root are equal - but this will get computationally expensive to build as the number of leaf nodes grows. The generation of a Merkle tree should only be done once to generate a root, and store the resulting proofs.

Advantage 2 - Logarithmic verification

Using the same methodology as before, we create the below tree with 8 nodes.

Note that there are 8 leaf nodes in this example but we only three proofs, three hash calculations and a string comparison for the root are required to do the same amount of computational effort.

It’s this reduction of data input needed to be submitted onchain by the user which is what makes verification so efficent at big N.

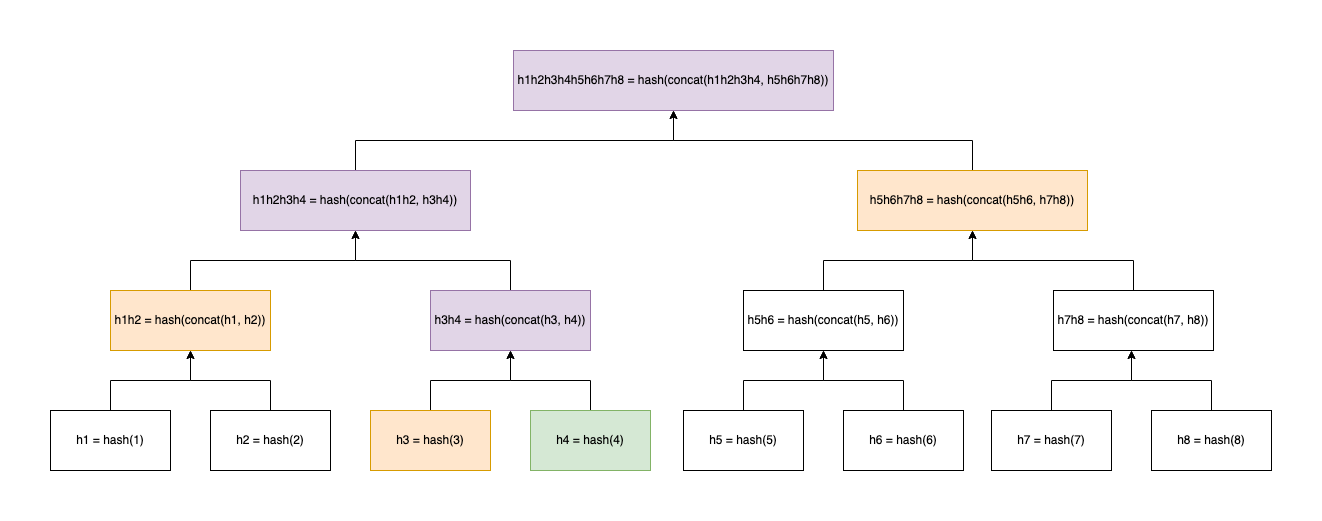Logarithmic searching reduces the computational spend.

Advantage 3 - Gas fees reduced for inserting rewards

Given that we have a Merkle root and we want to submit this onchain - we only need to provide one result hash of a fixed size costing a determinstic amount of gas, compared to adding rows linearly to a contract for the length of our input.

If we had thousands of users to reward or verify, computing and sending a linear amount of gas per operation is not efficent and will quickly bankrupt any funds or treasury you have to distribute these.

The below example shows the difference between the two models. The main pattern which is being used by these contracts are push vs pull. Do you push tokens to your user at a cost of gas, or do you make your users pull the rewards and offsetting some of that cost to them?

The current ZRC-2 and MerkleDistributor contracts model rewarding users with a fungible token with a Merkle tree.

Transfering has been a popular mechanism for airdrops but is wildly inefficent, naievely distributing tokens by iterating a collection in linear time and sending funds from A to B, costing the developer an gas amount linear to the amount of users in the collection.

The only upside for airdropping directly is that your users do not have to submit a transaction, which might be useful if your users don’t own any crypto or are lazy and won’t claim the reward, but the problem remains they will have no funds to interact with whatever you reward them with as they will be unable to pay the gas fees.

100 users

1000 users

*Variable depending on input byte length.

The conclusion we can draw from analysing the two distribution mechanisms is that the pull strategy is efficent as only one root is being submitted onchain, and it’s also negligable to ask to users to submit a transaction that costs a small amount of gas. Whereas the push mechanism can quickly scale out of control for large N.

Token Distributors

An example of when a Merkle tree is best used is in cryptocurrency token distributors. We can ensure unbiased processing of the computation and exeuction of rewards using smart contracts.

There are several reward concepts in crypto which require funds to be sent to users, either for participating in liquidity pools, defi or just holding an NFT. Since the Merkle contract just proves or disproves that a users proof is correct, you can enable mints, transfers and practically anything else you’d want to gatekeep.

One of the vectors of attack with a Merkle tree is the proof availability. If an attacker can disrupt where the proofs are being distributed from then users will be unable to claim their tokens. Decentralised storage mitigates nearly all of this risk. This isn’t such a problem for smaller projects, but larger projects can be majorly distrupted.

Introduction to Merkle trees on Zilliqa

Problem Statement - Reward users in LP with a fungible token

1
2
3

GIVEN some users are providing liquidity to a DEX where the state is a tuple of \<account, amount\>
WHEN some predetermined time has passed
THEN I want to reward everyone a fixed amount of tokens depending on their percentage allocated

This scenario is very common and can be modified to fit other scenarios such as holding a particular NFT or airdropping fungible tokens or NFTs.

We do need to take note of the rewarding timeframe. Too quickly and users will need to submit several transactions which may not be gas efficent for a small amount of tokens each time. Too long and your users will be annoyed at the frequency but will have a larger amount of tokens sent in a single transaction - which could have a negative impact on price performance. Targeting rewards for once a week seems to be the sweet spot which users don’t mind, all depends on how much gas is used and how much this costs on your chain of choice.

We want to take a snapshot of contract state every hour to track the state changes over the period of a week.

1

(1 snapshot * 24 hours) * 7 days = 168 snapshots

We’ll need to collect the LP data for each user and how much they have at the time of the snapshot.

We can then average the leafs into one final result set. From this result set we will have the average amount deposited over that period and how much of a percentage they own.

We will have a fixed amount of tokens we want to reward over this period, we can calculate how many tokens each user should get from knowing their percentage owned at each epoch.

Once we’ve summed and averaged all of the amounts, we’re left with a data structure like the below.

1
2
3
4
5
6
7
8
9
10
11
12

const b16Leaves = 
[
    {
        account:"0x00000000000000000000000000000000000000000",
        amount:"1000000000"
    },
    ...
    {
        account:"0x44444444444444444444444444444444444444444",
        amount:"44444444444"
    }
]

From here, we can generate a Merkle Tree which will contain all of the proof data and Merkle root.

1
2
3
4
5
6
7
8

const tree = generateTreeforBase16(b16Leaves)

// Print the rows of the tree
console.log(`Generated data for each input leaf`)
tree.data.map(p => console.log(p));

const merkleRoot = tree.getRoot().toString('hex')
console.log(`Root is : ${merkleRoot}`)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

{
  account: '0x00000000000000000000000000000000000000000',
  leaf: '0xa0054a1b7ede910bcddfe839cba8d43d07dea89a9c91b454b96f45ef8bb2cd96',
  amount: '1000000000',
  proof: [
    '0xa48e48a76785e90d65ba4b0f58772837b0514bcbda5611dd81200289e2a0fce8',
    '0xdbd48bc5ce7390e72d03b159a2dedec4f2258742d1dc4b6926031f516ff887a0',
    '0xc696f14bb8eb28f6fbaa5ae20303ce5107fed28c642f2221fb0a6a9d9afa7179'
  ]
},
{
  account: '0x11111111111111111111111111111111111111111',
  leaf: '0xc696f14bb8eb28f6fbaa5ae20303ce5107fed28c642f2221fb0a6a9d9afa7179',
  amount: '111111111',
  proof: [
    '0x6e5857651e652356e6291dc599bad97dcd8cd1192967c389c70cfbdb00b5d644',
    '0xd8d75c8c3566d53a4c20b847f6afda173be454939c3a49e6408dea748822e164',
    '0xc696f14bb8eb28f6fbaa5ae20303ce5107fed28c642f2221fb0a6a9d9afa7179'
  ]
}
...
Root is : 0x3ccb7ba4d737d6c618e864f19c8117e4f6fc934019bfc93fa0e2eb9c892ce655

The MerkleDistributor allows the Admin to post new roots to it. An example of this.

MerkleDistributor allows users to submit proofs with their inital dataset to check if the derived root is equal - it also let’s them batch multiple claims together. An example of this. (Notice the tokens being newly minted from the null address to the users wallet)

Once claimed, the Distributor stores a record in the state of the claimed leaf, so that repeated claims can be detected and identified to be hidden on the web client.

Summary

Merkle trees are becoming more common to see as developers don’t wish to pay for unnecessary gas costs, especially on chains where the native crypto is expensive.

The technicalities of Merkle trees can be easily hidden by web clients whereby they know nothing about the snapshots or the proofs they need to pass - it can be as simple as showing reward rows.